1. DFA & NFA with examples

DFA is the short form for the deterministic finite automata and NFA is for the Non-deterministic finite automata. Now, let us understand in detail about these two finite automata.

DFA

A Deterministic Finite automata is a five-tuple automata. Following is the definition of DFA −

M=(Q, Σ, δ,q0,F)

Where,

Q : Finite set called states.
Σ : Finite set called alphabets.
δ : Q × Σ → Q is the transition function.
q0 ϵ Q is the start or initial state.
F : Final or accept state.

NFA

NFA also has five states same as DFA, but with different transition function, as shown follows −

δ: Q X Σ → 2Q

Where,

Q : Finite set of states
Σ : Finite set of the input symbol
q0 : Initial state
F : Final state
δ : Transition function

Differences

The major differences between the DFA and the NFA are as follows −

Deterministic Finite Automata	Non-Deterministic Finite Automata
Each transition leads to exactly one state called as deterministic	A transition leads to a subset of states i.e. some transitions can be non-deterministic.
Accepts input if the last state is in Final	Accepts input if one of the last states is in Final.
Backtracking is allowed in DFA.	Backtracking is not always possible.
Requires more space.	Requires less space.
Empty string transitions are not seen in DFA.	Permits empty string transition.
For a given state, on a given input we reach a deterministic and unique state.	For a given state, on a given input we reach more than one state.
DFA is a subset of NFA.	Need to convert NFA to DFA in the design of a compiler.
δ : Q × Σ → Q For example − δ(q0,a)={q1}	δ : Q × Σ → 2Q For example − δ(q0,a)={q1,q2}
DFA is more difficult to construct.	NFA is easier to construct.
DFA is understood as one machine.	NFA is understood as multiple small machines computing at the same time.

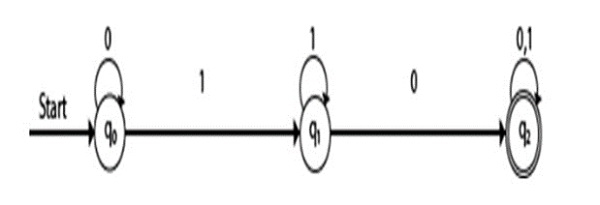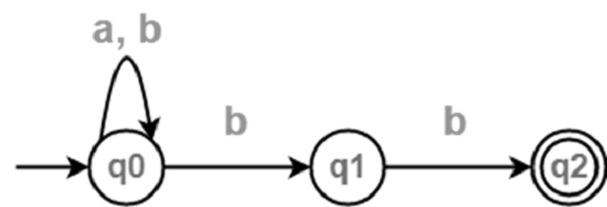2. Moore & Melay Machines with example

Finite automata may have outputs corresponding to each transition. There are two types of finite state machines that generate output −

Mealy Machine
Moore machine

Mealy Machine

A Mealy Machine is an FSM whose output depends on the present state as well as the present input.

It can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −

Q is a finite set of states.

∑ is a finite set of symbols called the input alphabet.
O is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
X is the output transition function where X: Q × ∑ → O
q0 is the initial state from where any input is processed (q0 ∈ Q).

The state table of a Mealy Machine is shown below −

Present state	Next state
	input = 0		input = 1
	State	Output	State	Output
→ a	b	x1	c	x1
b	b	x2	d	x3
c	d	x3	c	x1
d	d	x3	d	x2

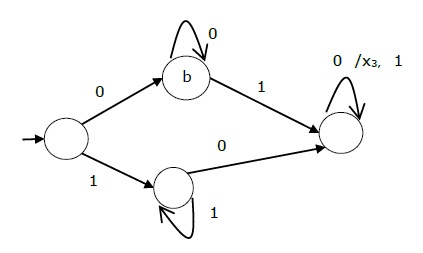
The state diagram of the above Mealy Machine is − State Diagram of Mealy Machine

Moore Machine

Moore machine is an FSM whose outputs depend on only the present state.

A Moore machine can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −

Q is a finite set of states.
∑ is a finite set of symbols called the input alphabet.
O is a finite set of symbols called the output alphabet.
δ is the input transition function where δ: Q × ∑ → Q
X is the output transition function where X: Q → O
q0 is the initial state from where any input is processed (q0 ∈ Q).

The state table of a Moore Machine is shown below −

Present state	Next State		Output
Present state	Input = 0	Input = 1	Output
→ a	b	c	x2
b	b	d	x1
c	c	d	x2
d	d	d	x3

The state diagram of the above Moore Machine is −

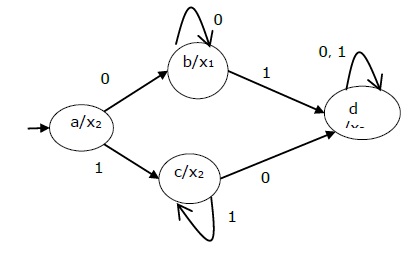
3.Construction of Finite Automata for Given RE

4. Construction of Regular Expression for the given DFA

5..Central concepts of Automata

This automaton consists of states and transitions. The State is represented by circles, and the Transitions is represented by arrows.

Automata is the kind of machine which takes some string as input and this input goes through a finite number of states and may enter in the final state.

There are the basic terminologies that are important and frequently used in automata:

Symbols:

Symbols are an entity or individual objects, which can be any letter, alphabet or any picture.

Example:

1, a, b, #

Alphabets:

Alphabets are a finite set of symbols. It is denoted by ∑.

Examples:

∑ = {a, b}
∑ = {A, B, C, D}
∑ = {0, 1, 2}
∑ = {0, 1, ....., 5]
∑ = {#, β, Δ}

String:

It is a finite collection of symbols from the alphabet. The string is denoted by w.

Example 1:

If ∑ = {a, b}, various string that can be generated from ∑ are {ab, aa, aaa, bb, bbb, ba, aba.....}.

A string with zero occurrences of symbols is known as an empty string. It is represented by ε.
The number of symbols in a string w is called the length of a string. It is denoted by |w|.

Example 2:

w = 010
Number of Sting |w| = 3

Language:

A language is a collection of appropriate string. A language which is formed over Σ can be Finite or Infinite.

Example: 1

L1 = {Set of string of length 2}

     = {aa, bb, ba, bb}          Finite Language

Example: 2

L2 = {Set of all strings starts with 'a'}

     = {a, aa, aaa, abb, abbb, ababb}         Infinite Language

6. Kleene Closure & Positive Closure

Closure properties on regular languages are defined as certain operations on regular language which are guaranteed to produce regular language. Closure refers to some operation on a language, resulting in a new language that is of same “type” as originally operated on i.e., regular.

Regular languages are closed under following operations.

Consider L and M are regular languages:

Kleen Closure:
RS is a regular expression whose language is L, M. R* is a regular expression whose language is L*.
Positive closure:
RS is a regular expression whose language is L, M. $R^+$ is a regular expression whose language is $L^+$ .

7. Identity Rules for Regular Languages :

8. Types of Grammers & Hierarchy:

Type 0: Unrestricted Grammar:

In Type 0
Type-0 grammars include all formal grammars. Type 0 grammar language are recognized by turing machine. These languages are also known as the Recursively Enumerable languages.

Grammar Production in the form of

$\alpha \to \beta$

where

$\alpha$ is ( V + T)* V ( V + T)*
V : Variables
T : Terminals.

$\beta$ is ( V + T )*.
In type 0 there must be at least one variable on Left side of production.

For example,

Sab –> ba
A –> S.

Here, Variables are S, A and Terminals a, b.

Type 1: Context Sensitive Grammar)
Type-1 grammars generate the context-sensitive languages. The language generated by the grammar are recognized by the Linear Bound Automata
In Type 1
I. First of all Type 1 grammar should be Type 0.
II. Grammar Production in the form of

$\alpha \to \beta$

| $\alpha$ | <= | $\beta$ |

i.e count of symbol in $\alpha$ is less than or equal to $\beta$

For Example,
S –> AB
AB –> abc
B –> b

Type 2: Context Free Grammar:
Type-2 grammars generate the context-free languages. The language generated by the grammar is recognized by a Pushdown automata.
In Type 2,
1. First of all it should be Type 1.
2. Left hand side of production can have only one variable.

| $\alpha$ | = 1.

Their is no restriction on $\beta$ .

For example,
S –> AB
A –> a
B –> b

Type 3: Regular Grammar:
Type-3 grammars generate regular languages. These languages are exactly all languages that can be accepted by a finite state automaton.

Type 3 is most restricted form of grammar.
Type 3 should be in the given form only :

V –> VT / T (left-regular grammar)

(or)

V –> TV /T (right-regular grammar)

for example:

S –> a

The above form is called as strictly regular grammar.

There is another form of regular grammar called extended regular grammar. In this form :

V –> VT* / T*. (extended left-regular grammar)
(or)
V –> T*V /T* (extended right-regular grammar)

for example :
S –> ab.

9 .LMD & RMD with examples

Left most derivation (LMD) and Derivation Tree: Leftmost derivation of a string from starting symbol S is done by replacing leftmost non-terminal symbol by RHS of corresponding production rule. For example: The leftmost derivation of string abab from grammar G above is done as:

 S => aSb => abSab => abab

The symbols underlined are replaced using production rules.

Right most derivation (RMD): Rightmost derivation of a string from starting symbol S is done by replacing rightmost non-terminal symbol by RHS of corresponding production rule. For Example: The rightmost derivation of string abab from grammar G above is done as:

S => SS => SaSb => Sab => aSbab => abab

The symbols underlined are replaced using production rules. The derivation tree for abab using rightmost derivation has been shown in Figure 2.

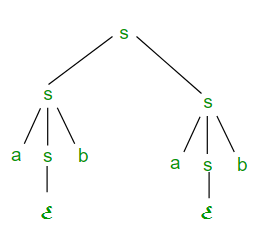
Ambiguity in Context free Grammar and Context free Languages2

Figure 2

A derivation can be either LMD or RMD or both or none. For Example:

S => aSb => abSab => abab is LMD as well as RMD

but S => SS => SaSb => Sab => aSbab => abab is RMD but not LMD.

10. Parse Tree

Parse tree

Parse tree is the graphical representation of symbol. The symbol can be terminal or non-terminal.
In parsing, the string is derived using the start symbol. The root of the parse tree is that start symbol.
It is the graphical representation of symbol that can be terminals or non-terminals.
Parse tree follows the precedence of operators. The deepest sub-tree traversed first. So, the operator in the parent node has less precedence over the operator in the sub-tree.

The parse tree follows these points:

All leaf nodes have to be terminals.
All interior nodes have to be non-terminals.
In-order traversal gives original input string

Example:

Production rules:

T= T + T | T * T
T = a|b|c

Input:

a * b + c

Flat imp question

1. DFA & NFA with examples

DFA

NFA

Differences

2. Moore & Melay Machines with example

Mealy Machine

Moore Machine

3.Construction of Finite Automata for Given RE

4. Construction of Regular Expression for the given DFA

5..Central concepts of Automata

Symbols:

Example:

Alphabets:

Examples:

String:

Example 1:

Example 2:

Language:

Example: 1

Example: 2

6. Kleene Closure & Positive Closure

7. Identity Rules for Regular Languages :

8. Types of Grammers & Hierarchy:

9 .LMD & RMD with examples

Parse tree

The parse tree follows these points:

Example:

Contact Form